In this vignette we discuss performance benchmarks of the Clarke-Wright algorithm implemented in this package by comparing the Clarke-Wright solutions of a set of problem instances (provided by CVRPLIB) with their optimal value.
We focus on two performance measures, which we call “scale-based performance” and simply “relative performance”.
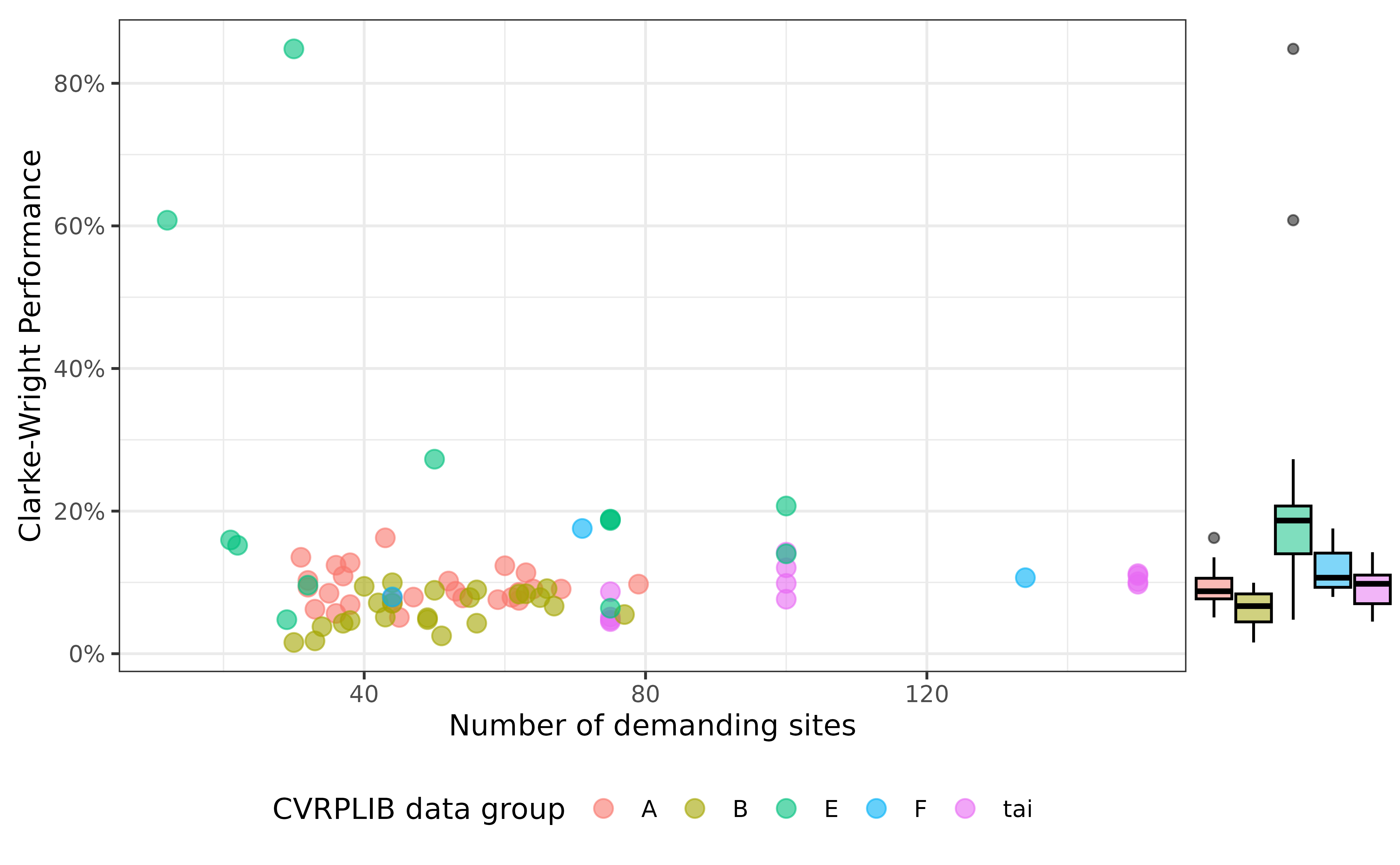
Scale based performance \(\xi\)
The idea of the scale based performance measure is to measure where the Clarke-Wright solution is compared to both, the optimal solution, and the trivial solution1. Let \(c\) be the cost of the Clarke-Wright solution, and \(o\) the optimal solution, and \(t\) the cost of the trivial solution. The measure \(\xi\) is defined by \[\xi := 1 - \frac{c - o}{t - o}\,.\] The measure can move between zero and 1. It is zero if the Clarke-Wright solution is the trivial solution, and it is 1 if the Clarke-Wright solution is the optimal solution.
Evaluating this for CVRPLIB sample data yields the following graph.
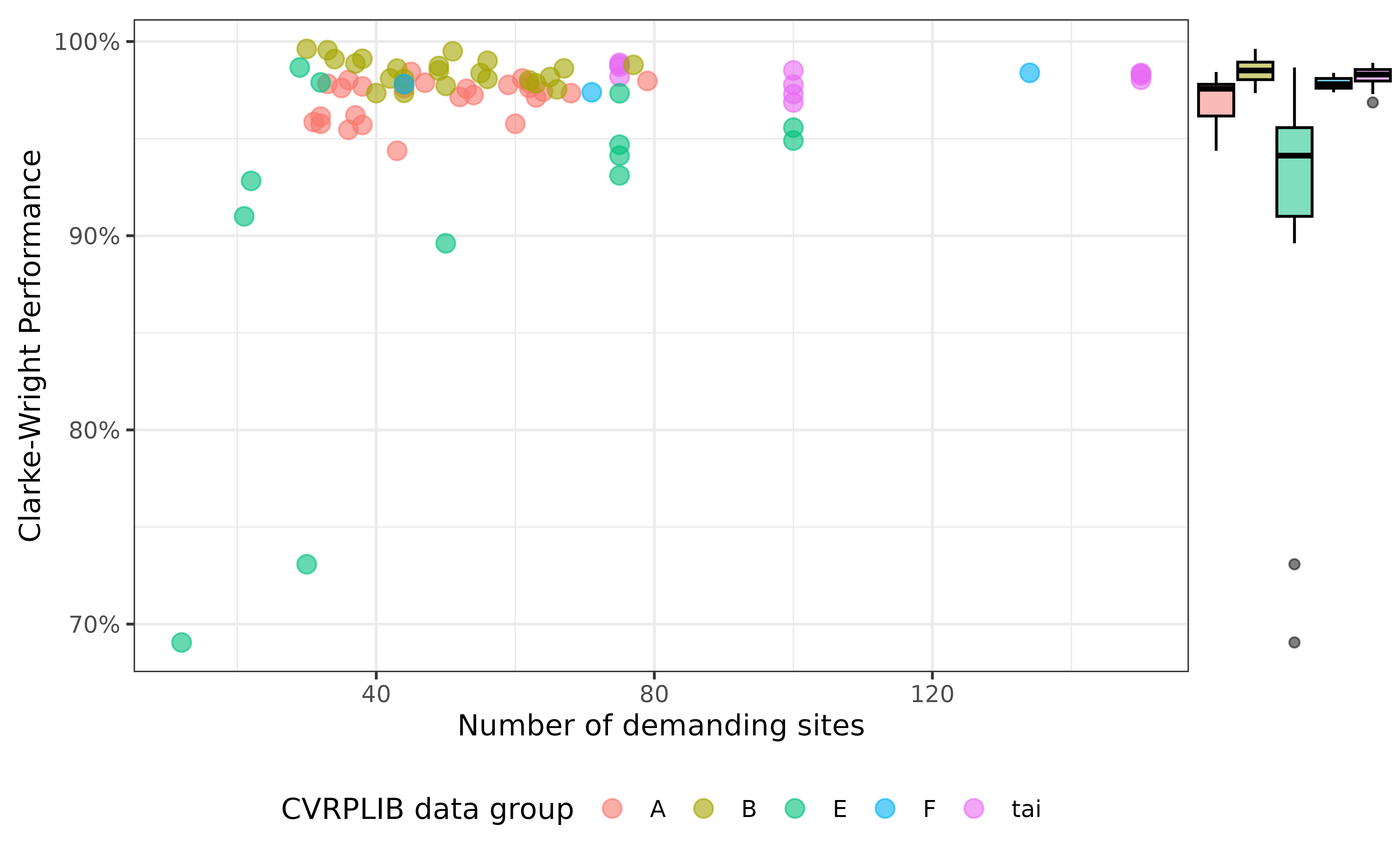
Relative performance \(\rho\)
We can also simply measure how far the optimal solution is away from the Clarke-Wright solution relative to the Clarke-Wright solution itself. \[\rho := 1 - \frac{c - o}{c}\,.\] The value \(\rho\) measures how much saving we missed by using the Clarke-Wright solution instead of the optimal solution.